너무나 당연한 이야기이지만 일변량 시계열 데이터는 단일 시간 종속 변수만 포함하고, 다변량 시계열 데이터는 다중 시간 종속 변수로 구성된다.
다변량 분석에서 예측할 변수의 과거의 데이터를 고려해야할 뿐만 아니라 여러 변수들 사이의 의존성을 고려해야 한다.
다변량 시계열 모델은 특정 주어진 데이터에 대해 더 신뢰성 있고 정확한 예측을 제공하기 위해 의존성을 이용해야 한다. 이번 글에서는 실제 데이터셋에 VAR(Vector Auto Regression)이라는 다변량 시계열 모델을 다뤄보자.
혼자 공부하고 이해할 때는 영어 그 자체로 충분했던 것들이 글을 쓰기 시작하면서 어떻게 한글로 써야 할까? 라는 의문이 들어서 중요한 용어들만 집고 넘어가고, 애매한 것들은 영어 원문으로 쓰기로 했다.
- univaritate time series - 일변량 시계열
- multivariate time series - 다변량 시계열
개발환경
- Python 3.6 이상
VAR(Vector Auto Regression) / 벡터 자동 회귀 분석이란?
VAR 모델은 예측할 변수의 과거 값뿐만 아니라 예측할 변수와 의존성이 있는 변수 들까지 고려하여 선형 함수로 나타내는 확률적 과정이다. 다음과 같은 시간당 온도와 풍속 사이의 관계를 과거 값의 함수로 설명하는 이변량 분석을 예로 들 수 있다.
온도(t) = a1 + w11* 온도(t-1) + w12* 바람(t-1) + e1(t-1)
바람(t) = a2 + w21* 온도(t-1) + w22*바람(t-1) + e2(t-1)
여기서 a1과 a2는 상수이고 w11, w12, w21, w22는 계수 e1과 e2는 오차항이다.
데이터셋
이번에는 주로 사용하지 않았던 statsmodels python api를 사용해보고자 한다. statsmodels은 사용자가 데이터를 탐색하고 통계적 모델을 추정하며 통계적 테스트를 수행할 수 있게 도와주는 API이다. 시계열 데이터도 포함하고 있다.
우선 필요 모듈 임포트부터 하고
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
import pandas as pd
import statsmodels.api as sm
from statsmodels.tsa.api import VAR
from statsmodels.tsa.stattools import adfuller
데이터를 다운로드하기 위해서는 파이썬 스크립트 내에서 다음과 같이 입력하면 된다.
data = sm.datasets.macrodata.load_pandas().data
data.head()
출력 결과는 다음과 같다.

데이터셋에는 시계열 데이터가 들어있는데, 우리는 이중에 year, realgdp, realdpi 세가지만 사용해보자.
mydata = data[["realgdp", 'realdpi']]
mydata.index = data["year"]
mydata.head()
시각화 한번 해주고.
mydata.plot(figsize = (8,5))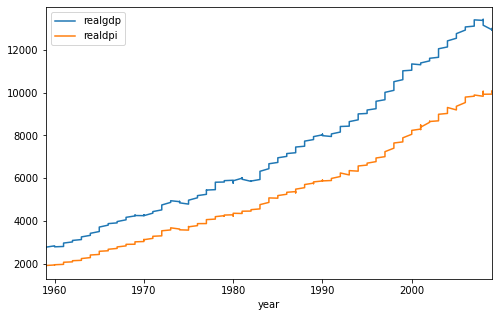
두 시계열 데이터 모두 시간이 갈수록 상승하는 추세를 보여준다.
Stationary time series / 정상성
stationary라는 뜻은 정적이라는 뜻이다. 또한 stationarity라 정상성이란 뜻인데, 데이터가 정상성을 가진다는 의미는 데이터의 평균과 분산이 안정되어 있어 분석하기 쉽다는 의미이기도 하다. 통상적으로 평균이 일정하지 않으면 차분을 취하고, 분산이 일정하지 않으면 변환을 취한다.
VAR을 적용시켜보기 전에 두 시계열 변수가 모두 stationay 상태이어야 한다. 두 시계열 데이터가 일정한 평균과 분산을 나타내지 않기 때문에 두 변수는 unstationay 상태이다. AIC 기준을 사용하여 데이터의 stationarity를 찾기 위해 ADF(Advanced Dickey-Fuller test)와 같은 통계적 테스트를 수행해보자.
adfuller_test = adfuller(mydata['realgdp'], autolag= "AIC")
print("ADF test statistic: {}".format(adfuller_test[0]))
print("p-value: {}".format(adfuller_test[1]))
>> ADF test statistic: 1.7504627967647168
>> p-value: 0.9982455372335032
adfuller_test = adfuller(mydata['realdpi'], autolag= "AIC")
print("ADF test statistic: {}".format(adfuller_test[0]))
print("p-value: {}".format(adfuller_test[1]))
>> ADF test statistic: 2.986025351954683
>> p-value: 1.0
두 경우 모두 p-value가 충분히 유의미한 값을 가지지 않아 귀무가설(null hypothesis)을 기각할 수 없고 시계열 데이터가 non-stationary라고 결론을 내릴 수 있다는 의미이다.
* p-value의 의미를 어떻게 해석하는지는 따로 정리를 해야 할 예정
differencing / 차분
두 시계열 데이터는 모두 stationary 상태가 아니기 때문에 차분을 취하고 나서 stationary를 확인해보자
아래와 같이 입력해서 차분을 구해주고
mydata_diff = mydata.diff().dropna()
다시 확인해보면?
adfuller_test = adfuller(mydata_diff['realgdp'], autolag= "AIC")
print("ADF test statistic: {}".format(adfuller_test[0]))
print("p-value: {}".format(adfuller_test[1]))
>> ADF test statistic: -6.305695561658106
>> p-value: 3.327882187668224e-08
adfuller_test = adfuller(mydata_diff['realdpi'], autolag= "AIC")
print("ADF test statistic: {}".format(adfuller_test[0]))
print("p-value: {}".format(adfuller_test[1]))
>> ADF test statistic: -8.864893340673008
>> p-value: 1.4493606159108096e-14
realgdp, realdpi 모두는 p-value 값이 꽤나 작아졌다. sationary 상태가 되었다.
Modeling / 모델링
우선 데이터를 트레인/테스트 셋으로 나누어주자
마지막 10일은 test 나머지는 train이다.
train = mydata_diff.iloc[:-10,:]
test = mydata_diff.iloc[-10:,:]
VAR모델의 최적 순서 찾아보기
VAR 모델링 과정에서, 최적의 모델을 찾기 위한 기준 AIC(Akaike's Information Criterion)를 모델 선택 기준으로 하자.
간단히 말해서, 최상의 AIC점수를 바탕으로 VAR의 순서(p)를 선택한다. AIC는 일반적으로 모델이 너무 복잡하다는 이유로 불이익을 주곤 하는데 복잡한 모델은 일부 다른 모델 선택 기준에서 약간 더 나은 성능을 보여 줄 수 있다. 따라서 순서(p) 검색 시 변곡점이 예상되는데, 이는 일정 순서가 될 때까지 순서 p가 커지면 AIC점수가 감소하고, 이후 점수가 높아지기 시작한다는 것을 의미한다.
grid-search를 수행해서 최적의 p를 조사해보자.
forecasting_model = VAR(train)
results_aic = []
for p in range(1,10):
results = forecasting_model.fit(p)
results_aic.append(results.aic)
위 코드의 첫 번째 줄에서 VAR 모델을 학습시킨다. 나머지 줄에서는 1부터 10까지 적합한 순서에 대한 AIC 점수를 찾기 위해 반복문을 통해 grid-search를 한다.
이 값을 시각화해보자.
sns.set()
plt.plot(list(np.arange(1,10,1)), results_aic)
plt.xlabel("Order")
plt.ylabel("AIC")
plt.show()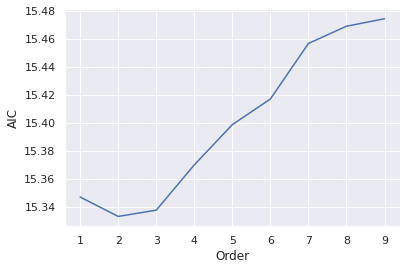
결과 그래프에서 가장 낮은 AIC점수는 2이고, 그 이후 p가 커짐에 따라 증가 추세를 보인다. 따라서 VAR모델의 최적 순서는 2로 선택한다. 예측 모형에 순서 2로 fit 시키고 요약 결과를 살펴보자.
results = forecasting_model.fit(2)
results.summary()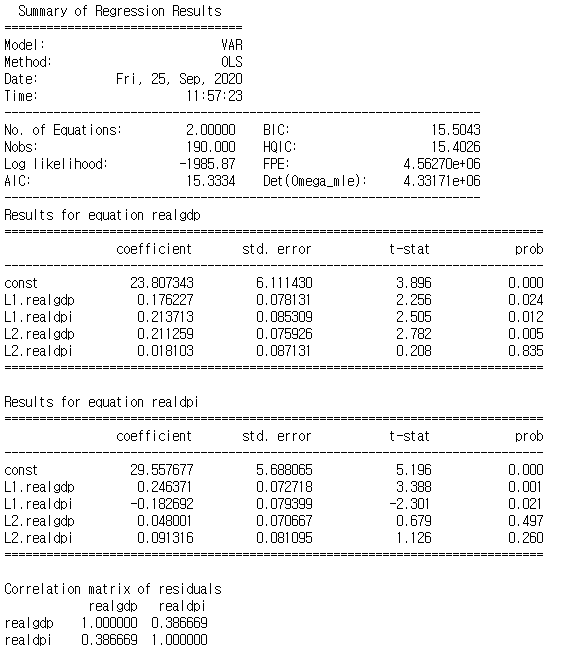
Forcasting / 예측하기
위에서 도출한 것처럼 VAR모델을 맞추는데 최적의 순서로 2를 사용한다. 학습된 모델에 2일 동안의 훈련을 넣어 향후 10일 동안의 테스트 데이터를 예측해보자.
laaged_values = train.values[-2:]
forecast = pd.DataFrame(results.forecast(y= laaged_values, steps=10), index = test.index, columns= ['realgdp_1d', 'realdpi_1d'])
forecast
앞서 언급한 예측이 차분(diffencing)에 대한 모델에 대한 것이라는 점을 유념해야 한다.
차분을 더하여 우리가 예측해야 할 값으로 만들어주자.
forecast["realgdp_forecasted"] = mydata["realgdp"].iloc[-10-1] + forecast['realgdp_1d'].cumsum()
forecast["realdpi_forecasted"] = mydata["realdpi"].iloc[-10-1] + forecast['realdpi_1d'].cumsum()
forecast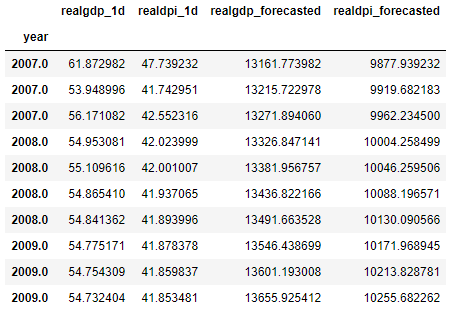
왼쪽 두열(_1d)은 차분에 대한 예측값이고 오른쪽 두열(_forcasted)은 원래 시리즈에 대한 예측값이다.
실제 test 셋과 합쳐서 시각화해보자.
test = mydata.iloc[-10:,:]
test["realgdp_forecasted"] = forecast["realgdp_forecasted"]
test["realdpi_forecasted"] = forecast["realdpi_forecasted"]
test.plot()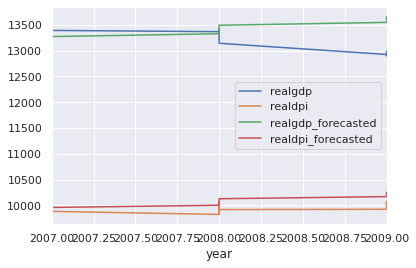
아래 두줄 realdpi와 realdpi_forecasted는 비슷한 패턴을 보여준다.
위 두줄 realgdp와 realgdp_forecasted는 절반 정도는 비슷하다가 다른 패턴을 보여준다.
요약하자면
간단하게 다변량 시계열 분석에 대해 알아보았고 VAR을 실제 다변량 시계열 데이터셋에 적용해보았다.
일변량 분석에 대해 알고 싶다면 여기에 facebook의 prophet 라이브러리를 활용한 글이 있으니 참고.
요즘 월급쟁이로 자본주의를 졸업할 수 없다는 것을 알게 된 후 이리저리 돈 벌 궁리를 하는 중인데 시계열 머신러닝을 좀 심도 있게 학습한 후에 주택이나 환율 예측을 해보는 장기 프로젝트를 진행해볼까 싶다.
'ML | DL | Big data > ML' 카테고리의 다른 글
| 시계열 예측을 지도 학습으로 바꾸는 방법 - Time Series to Supervised Learning with Sliding window (1) | 2020.09.11 |
|---|---|
| Python Prophet - 자동차 판매량 시계열 데이터 예측하기(Time Series Forecasting) (3) | 2020.08.28 |
| XGBoost (4) - 머신러닝으로 부동산 가격 예측 실습하기 / Tutorial (0) | 2020.07.14 |
| XGBoost (3) - Python 가상 환경에 설치하기 (0) | 2020.07.13 |
| XGBoost (2) - Parameter 이해와 현업자의 설정 방법 (2) | 2020.07.09 |
| XGBoost (1) - 입문용 예제로 개념 쉽게 이해하기 (0) | 2020.07.08 |




댓글