오늘은 Skew와 Kurtosis, 즉 왜도와 첨도에 대해서 알아보자.
Skewness / 왜도
symmetrical bell curve 혹은 normal distribution에서 왜곡 정도를 말한다. 데이터 분포의 대칭성이 얼마나 결핍되었는지를 측정한다. 완전히 대칭인 분포는 skewness가 0이다.
두 가지 종류의 Skewness가 있다. Positive와 Negative
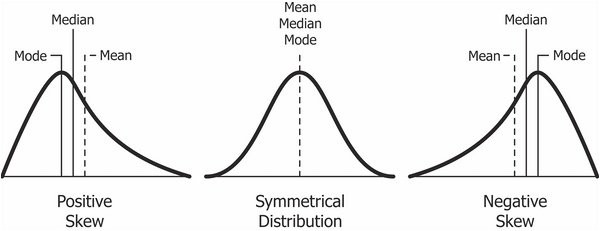
Positive Skewness는 오른쪽 꼬리가 왼쪽보다 더 길 때를 의미한다. 평균(Mean)과 중위수(Median)가 Mode보다 크다.
Negative Skewness 왼쪽 꼬리가 오른쪽보다 더 길 때를 의미한다. 평균(Mean)과 중위수(Median)가 Mode보다 작다.
그래서, 언제 Skewness(왜도)가 과도하게 커질까?
경험에 근거한 법칙은 다음과 같다.
- skewness가 -0.5 ~ 0,5 일 경우 데이터는 상당히 대칭적이다.
- skewness가 -1~-0.5 이거나 0.5~1 일 경우 데이터는 적당히 치우쳐있다.
- skewness가 -1보다 작거나 1보다 클 경우 데이터는 상당히 치우쳐있다.
예시
흔한 집값을 예로 들면. 1억 원 ~ 10억 원 사이의 주택들의 데이터가 있다고 가정하자.
분포의 피크가 평균값에서 왼쪽에 있을 경우 분포의 Positive Skewness이다. 그 말은 즉슨 많은 집들이 평균값, 즉 5억 원(정확히는 5.5억) 이하의 가격에 팔리고 있다는 것을 의미한다.
분포 피크가 평균값과 보다 오른쪽에 있다면 이는 Negative Skewness을 의미한다. 집들이 평균값보다 더 높은 가격으로 많이 팔리고 있다는 것을 의미한다.
Kurtosis / 첨도
첨도는 분포 그래프의 꼬리 부분에 관한 것이다. 정점(peakness)이나 평탄도(flatness)가 아니다. 극단적인 값들을 한 꼬리와 다른 꼬리로 설명하는 데 사용된다. 분포에 존재하는 특이치(outlier)의 척도다.
Kurtosis가 높으면 데이터가 두꺼운 꼬리나 outlier를 가지고 있다는 것을 의미하는 지표이다. 왜 이렇게 많은 outlier를 가지고 있는지 조사할 필요가 있다. 어쩌면 잘못된 데이터 입력이나 다른 것들이 있을 수 있다. 조사해보자!
Kurtosis가 낮으면 데이터가 얇은 꼬리나 outlier를 가지고 있지 않다는 듯이다. 만약 낮은 첨도가 나온다고 해도 이상 결과의 데이터를 다듬을 필요가 있다.

Mesokurtic : 이 분포는 정규 분포와 유사한 첨도 통계량을 가지고 있다. 분포의 극단값이 정규 분포 특성과 유사하다는 뜻이다. 표준 정규 분포는 3의 첨도 갖는다.
Leptokurtic (Kurtosis > 3) : 분포가 길고, 꼬리가 더 뚱뚱하다. 피크는 Mesokurtic보다 높고 날카롭기 때문에 데이터는 꼬리가 무겁거나 특이치(outlier)가 많다는 것을 의미한다.
특이치(outlier)는 히스토그램 그래프의 수평 축을 확장하여 데이터의 대부분이 좁은 수직 범위로 나타나도록 하여 Leptokurtic 분포의 "skinniness"을 부여한다.
Platykurtic (Kurtosis < 3) : 분포는 짧고 꼬리는 정규 분포보다 얇다. 피크는 Mesokurtic보다 낮고 넓으며, 이는 데이터가 가벼운 편이나 특이치(outlier)가 부족하다는 것을 의미한다.
이유는 극단값(extream value)이 정규 분포의 극단값보다 작기 때문이다.
Reference
'ML | DL | Big data > Data Science' 카테고리의 다른 글
| 통계적 가설 검정 방법 (0) | 2023.02.28 |
|---|---|
| 빅데이터 개요 (0) | 2023.02.28 |
| 불균형 클래스 분류(Imbalanced Classification)를 위한 4가지 방법 (2) | 2020.09.04 |
| 누락 데이터(Missing value)를 처리하는 7가지 방법 / Data Imputation (2) | 2020.08.14 |
| 비대칭(skewed) 데이터를 처리하는 3가지 방법 / Skewed Data (2) | 2020.08.13 |
| 데이터 과학자가 꼭 알아야 할 5분 통계학 (0) | 2020.08.11 |




댓글